Transformer

Updated on Feb 17
Updated on Feb 18 – completed neural network part
Update on Mar 2 – completed transformer part

1. 机器学习的原理

• 定义：A computer learns from experience E regarding task T according to some performance P measured by improvement with E
  • 贴好分类标签的邮件集合E，学习 T = 如何将邮件进行分类，衡量标准是正确分类的比例 P = 正确分类的比例
  • Training set, T – Conduct Forecast, P – Performance on T measured by improvement with E
• Model Representation
  • Test set 包含样本: x_1和标签: y_1
  • 模型: f, 希望训练一个能回答问题的模型，也即y = f(x)，输入问题，输出答案; 学习input features和output labels之间的关联
    • 模型的参数: f(θ), θ是参数
    • “给分”: loss，用来训练模型，即改变θ的值

1.1 Supervised learning

特征是labeled dataset

1. Inputs:

x_j^{(i)} = \text{value of feature } j \text{ in the } i^\text{th} \text{ training example}

training set 有m个sample，代表x^{(i)}的i∈[1,m]，X是m×n的矩阵；模型有n个参数，代表j∈[1,n], θ是1×n的矩阵

2. Models

1. Linear function: 简单线性方程
   h_\theta(x) = \theta x = \begin{bmatrix} \theta_1 & \theta_2 & \cdots & \theta_n \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}
2. Sigmoid function: 逻辑回归，输出值为[0,1]之间的概率值；若概率值大于等于0.5则预测标签为1，小于时为0。但阈值可以灵活调节，比如医学中可能需要0.7
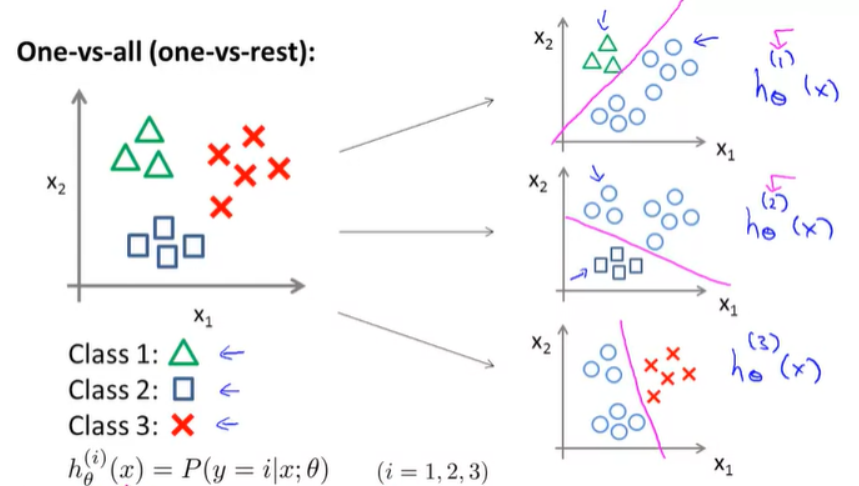
   h_θ(x) = g(θ^Tx) = \frac {1}{1+e^{(-θ^Tx)}}
3. Multiclass classification – 多分类回归
   • One-vs-all, 等价于对于每个类别训练一个二分类模型，将类别i视为正类，其他所有类别视为负类。
     h_\theta^{(i)} = P(y=i \mid x;\theta) 表示在给定 \theta 和 X 的前提下，样本属于类别 i 的概率。
   • 选择概率最大的作为预测结果：\text{predicted class} = \arg\max_i h_\theta^{(i)}(x)
     

3. cost function

Cost function是机器学习中用于衡量模型预测值与真实值之间差异的函数
– 一个关于参数的函数而不是inputs的
– 本质上可以有不同的Cost Function，这里使用的是最简单的：差平方和的平均值

J(\theta_0, \theta_1) = \frac{1}{2m} \sum_{i=1}^{m} \left( h_{\theta}(x^{(i)}) – y^{(i)} \right)^2

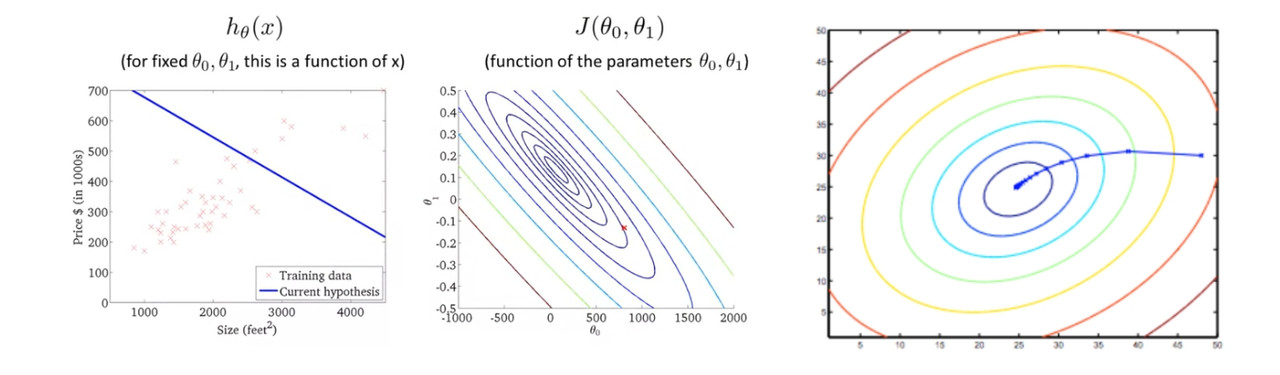
4. Gradient Descent

梯度下降是一种优化算法，用于最小化cost function。选定一套初始θ开始求J, 然后通过根据选定步长来不断调整参数\theta使得J(\theta)逐步接近最小值

\theta_j := \theta_j – \alpha \frac{\partial}{\partial \theta_j}J(\theta) = \theta_j – \alpha\frac{1}{m}\sum_{i=1}^{m} \left( h_{\theta}(x^{(i)}) – y^{(i)} \right)x^{(i)}

i 是随机选择的一个样本索引
\alpha: Learning rate决定了每一步的size, \alpha 太大的后果可能是J会反而增大，如果太小则收敛速度太慢；一旦选定后需要保持constant
当derivative = 0的时候达到Local optimum

1.2 Machine learning vs. Matrix solving

Matrix solving:
y = X\theta = \begin{bmatrix} x^{(1)} \ x^{(2)} \ \vdots \ x^{(m)} \end{bmatrix} \begin{bmatrix} \theta_1 \ \theta_2 \ \vdots \ \theta_n \end{bmatrix} = \begin{bmatrix} 1&x_1^{(1)}&x_2^{(1)}&\cdots&x_n^{(1)} \ 1&x_1^{(2)}&x_2^{(2)}&\cdots&x_n^{(2)} \ \vdots&\vdots&\vdots&\ddots&\vdots \ 1&x_1^{(m)}&x_2^{(m)}&\cdots&x_n^{(m)} \end{bmatrix} \begin{bmatrix} \theta_1 \ \theta_2 \ \vdots \ \theta_n \end{bmatrix}
要得到θ值：计算复杂，需要消耗的资源非常多

\theta = (XX^T)^{-1}X^Ty， ~O(n^3)

但machine learning可以降低复杂度到 O(kmn):每次更新值计算一个样本的梯度，计算量大大减少，适合大规模数据集的计算效率

• 矩阵求解法和梯度下降法最终会得到相同的解，原因如下：
  • 目标函数相同：矩阵求解法和梯度下降法都是在最小化相同的损失函数（均方误差）。矩阵求解法是通过解析解直接找到全局最小值，而梯度下降法是通过迭代逐步逼近全局最小值。
  • 凸优化问题：线性回归的损失函数 J(θ) 是一个凸函数，只有一个全局最小值。无论是矩阵求解法还是梯度下降法，最终都会收敛到这个全局最小值。

2. 神经网络

• 神经网络由 input layer – hidden layers – output layer 构成
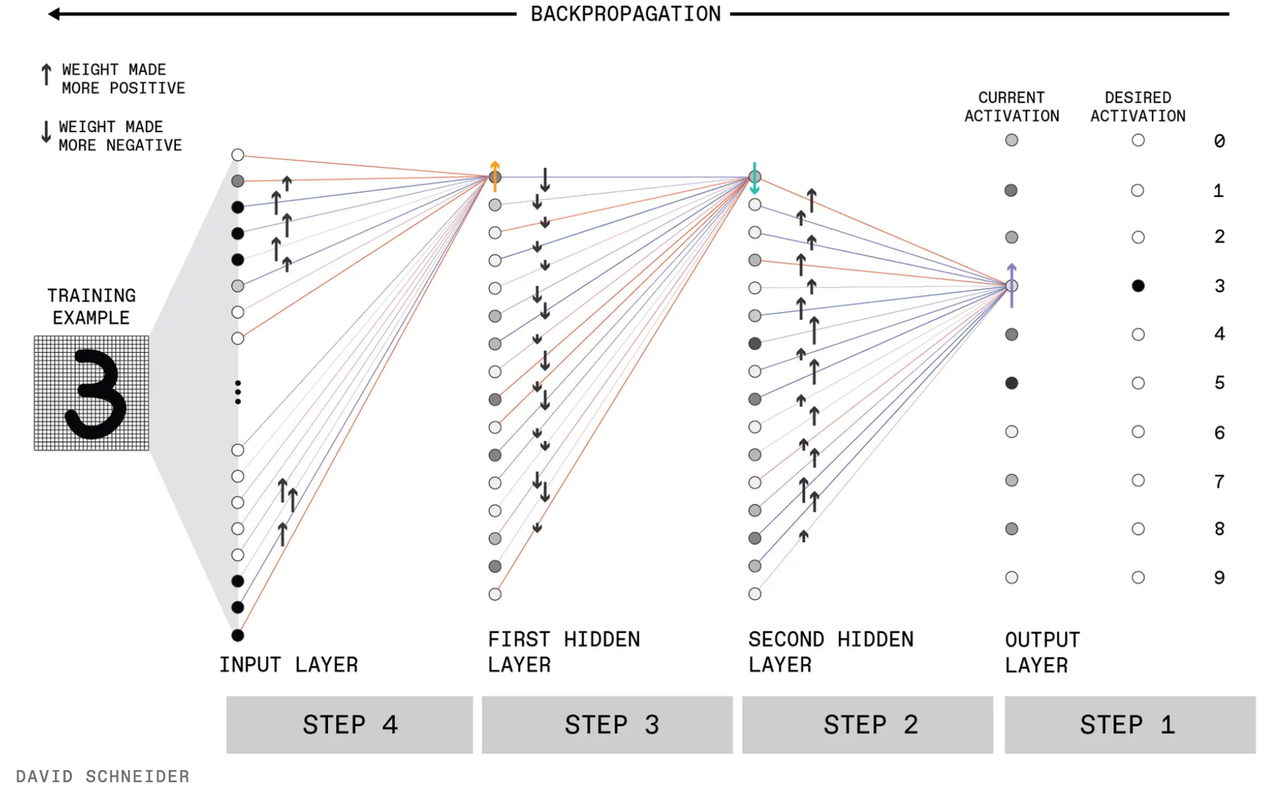
  举例说明：识别数字0-9的神经网络

1. Inputs
   • 含义：数值输入，如图像的像素点、分类的0-1值或文本的embedding vectors。
   • 例子中的具体行业操作：图像输入通常是由多个像素点组成，如(28^2 = 784)个像素点，作为输入层的节点。对于文本，输入通常是词嵌入向量，表示每个词的特征。
2. Hidden Layer
   • 含义：每个隐藏层有一个权重矩阵，与上一层的输入共同计算输出的激活值。
   • 解释：每个隐藏层的输出是通过对上一层的输出与当前层权重矩阵的乘积，再加上偏置项，然后通过激活函数计算得到的。具体为 (\Theta^{(l)} \cdot X + b^{(l)}) 后再通过激活函数 (g) 得到激活值。
   • 例子中的具体行业操作：在神经网络中，隐藏层的节点数和结构通常是根据任务需求确定的，层与层之间通过权重矩阵连接。
3. Activation Value
   • 含义：每个神经元激活函数的输出值，通常是一个概率。
   • 解释：每个神经元的激活值是通过将上一层的加权输入传递给激活函数（如sigmoid或ReLU）来计算的。激活函数的目的是引入非线性，帮助网络学习复杂的模式。
   • 例子中的具体行业操作：假设第二层的输出是 \begin{bmatrix}a_1^{(2)} \\ a_2^{(2)} \\ \vdots \\ a_{l_2}^{(2)}\end{bmatrix} = g\left( \Theta^{(1)}X \right))，表示每个隐藏层神经元的激活值。
4. Activation Function
   • 含义：用于将输入转化为下一个层的输出的函数，通常是非线性的。
   • 解释：激活函数的作用是为网络引入非线性特性，使得神经网络可以学习和表示复杂的关系。常见的激活函数有Sigmoid、ReLU、Tanh等。Sigmoid函数将输出值压缩到(0, 1)之间，适用于二分类任务。
   • 例子中的具体行业操作：使用sigmoid函数时，输出将会被限制在(0, 1)之间，常用于分类问题的输出层。
5. Outputs
   • 含义：神经网络最后一层的输出，通常表示分类的概率。
   • 解释：网络的输出通常表示每个类别的概率，通常经过激活函数处理，转换为可以作为分类结果的概率值。在多分类任务中，通常使用Softmax函数将每个类别的得分转化为概率。
   • 例子中的具体行业操作：对于图像分类任务，网络的最终输出可能是一个概率分布，表示图像属于每个可能类别的概率。

其中权重矩阵的公式为：
\Theta^{(1)} = \begin{bmatrix}\theta_{11}^{(1)}&\theta_{12}^{(1)}&\cdots&\theta_{1n}^{(1)} \ \theta_{21}^{(1)}&\theta_{22}^{(1)}&\cdots&\theta_{2n}^{(1)} \ \vdots&\vdots&\ddots&\vdots \ \theta_{l_2,1}^{(1)}&\theta_{l_2,2}^{(1)}&\cdots&\theta_{l_2,n}^{(1)}
\end{bmatrix}

• $\Theta^{(1)}$ 是从输入层到第一隐藏层的权重矩阵。其大小为 $[l_2 \times n]$，其中 $l_2$ 是第一隐藏层神经元的数量，$n$ 是输入特征的数量（即输入层节点数）。
• 每个 \theta_{ji}^{(1)} 表示从输入节点 i 到隐藏层神经元 j 的权重。

• 然后，加权输入可以通过以下公式表示：\Theta^{(1)} X
  • $X$ 是输入数据矩阵，大小为 $n \times m$，其中 $n$ 是输入特征的数量，$m$ 是样本数量。
  • $\Theta^{(1)} X$ 的结果是一个 $l_2 \times m$ 的矩阵，表示每个样本经过权重变换后的加权输入。

Backwards propagation

1. 初始化权重
随机初始化权重矩阵 \theta_{ji}^{(l)}，其中 l 表示第 l 层，j 表示第 j 个神经元，i 表示前一层第 i 个神经元的输入。
注意，我们用z来表示最后输出层的权重。
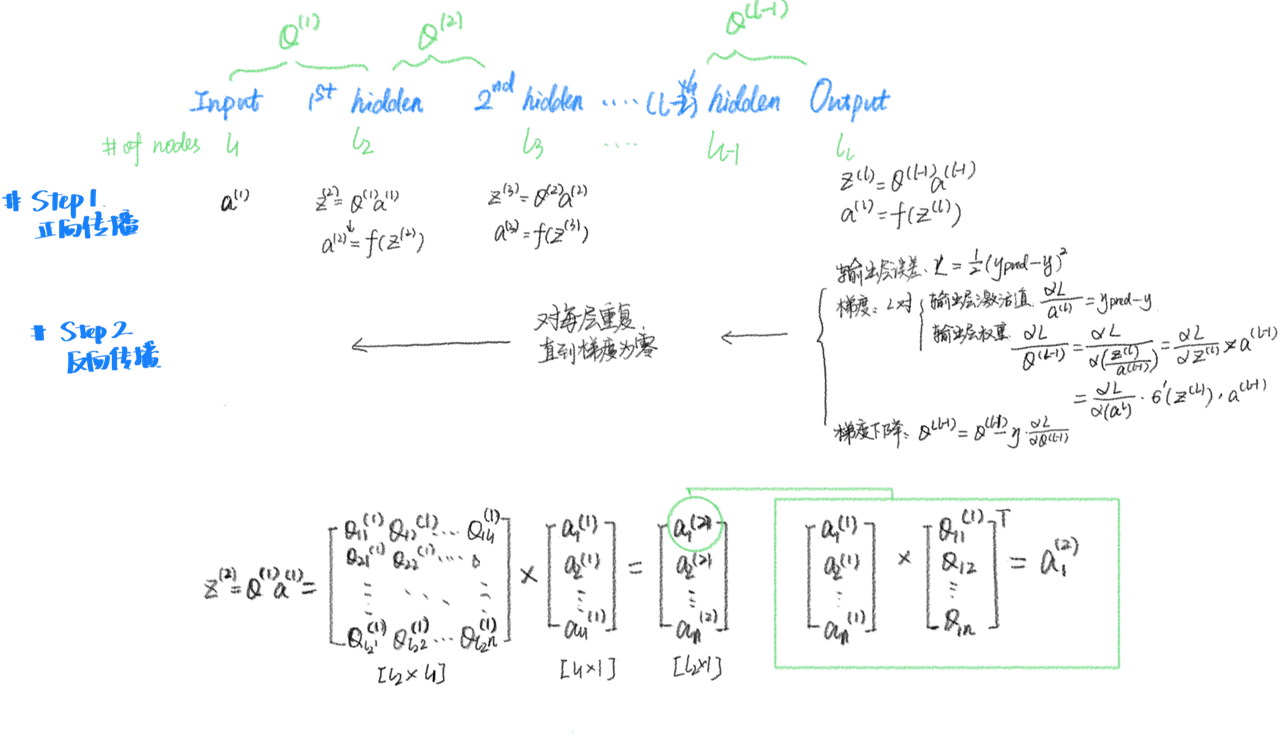
2. 前向传播
通过前向传播计算每一层的激活值（activation value）：
– 第 l 层的线性变换：
z^{(l)} = \theta^{(l)} a^{(l-1)} + b^{(l)}
其中：a^{(l-1)} 是第 l-1 层的激活值，b^{(l)} 是偏置项。
– 第 l 层的激活值：
a^{(l)} = \sigma(z^{(l)})
其中 \sigma 是激活函数（如 Sigmoid、ReLU）。
3. 计算输出层误差
计算输出层的误差（以均方误差为例）：
L = \frac{1}{2} (y_{\text{pred}} – y_{\text{true}})^2
其中：y_{\text{pred}} 是网络的预测输出，y_{\text{true}} 是真实标签。

4. 反向传播
反向传播通过链式法则从输出层向输入层逐层计算梯度，并更新权重。
(1) 计算输出层的梯度
– 损失函数对输出层激活值 a^{(L)} 的梯度：
\frac{\partial L}{\partial a^{(L)}} = y_{\text{pred}} – y_{\text{true}}
– 损失函数对输出层线性变换 z^{(L)} 的梯度：
\frac{\partial L}{\partial z^{(L)}} = \frac{\partial L}{\partial a^{(L)}} \cdot \sigma'(z^{(L)})
其中 \sigma’ 是激活函数的导数。
– 损失函数对输出层权重 \theta^{(L)} 和偏置 b^{(L)} 的梯度：
\frac{\partial L}{\partial \theta^{(L)}} = \frac{\partial L}{\partial z^{(L)}} \cdot a^{(L-1)}
\frac{\partial L}{\partial b^{(L)}} = \frac{\partial L}{\partial z^{(L)}}
(2) 计算隐藏层的梯度
对于第 l 层（从 L-1 到 1）：
– 损失函数对第 l 层激活值 a^{(l)}的梯度：
\frac{\partial L}{\partial a^{(l)}} = \theta
– 损失函数对第 l 层线性变换 z^{(l)} 的梯度：
\frac{\partial L}{\partial z^{(l)}} = \frac{\partial L}{\partial a^{(l)}} \cdot \sigma'(z^{(l)})
– 损失函数对第 l 层权重 \theta^{(l)} 和偏置 b^{(l)} 的梯度：
\frac{\partial L}{\partial \theta^{(l)}} = \frac{\partial L}{\partial z^{(l)}} \cdot a^{(l-1)}
\frac{\partial L}{\partial b^{(l)}} = \frac{\partial L}{\partial z^{(l)}}

(3) 更新参数
使用梯度下降法更新每一层的权重和偏置：
\theta^{(l)} = \theta^{(l)} – \eta \cdot \frac{\partial L}{\partial \theta^{(l)}}
b^{(l)} = b^{(l)} – \eta \cdot \frac{\partial L}{\partial b^{(l)}}
其中 \eta 是学习率。

5. 循环训练
重复前向传播和反向传播，直到损失函数收敛。

Summary

2. Transformer

1.Encoder的结构：

1. 一个encoder和一个decoder
2. encoder有一个多头，而decoder有两个
3. 每个多头都有多个self-attention, 以及一个feed forward, 每个self-attention和feed forward都有一个add&norm

在Transformer的Encoder中，每一层的结构通常是：
输入
│
Self-Attention
│
Add & Norm（残差连接 + 归一化）
│
Feed Forward（前馈神经网络）
│
Add & Norm（残差连接 + 归一化）
│
输出

1） Input矩阵X：Embedding

• 用一套embedding的法则将输入语言转化为向量矩阵：
  • 每个单词转化为一个向量 ，这个向量由两个向量组成：一个代表提取特征的词向量，一个代表单词位置的位置向量。
  • 转化embedding的机制有很多种，比如Word2Vec
  • Input矩阵X的维度为：d_{token} \times d_{model}, 其中d_{token}是单词的数量，而d_{model}是由embedding机制所决定的。

2）Self-attention

注意理解self和attention
self attention的输入是Query（Q），键值key（K），以及值Value（V)

• Step 1: X \times W_{q} = Q query matrix

  q^{(i)}=x^{(i)} \times W_q represents a word

  X(d_{token}, d_{model}) \times W_q(d_{model},d_q) = Q(d_{token},d_q)

• Step 2: X \times W_{k} = K key value matrix

  k^{(i)}=x^{(i)} \times W_k represents a word

  X(d_{token}, d_{model}) \times W_k(d_{model},d_k) = K(d_{token},d_k)

• Step 3: Q \times K^T = attention scores matrix

  X(d_{token}, d_q) \times W_k(d_k,d_{token}) = A(d_{token},d_{token})

  所以每个词都算出了和自己的self attention scores
  事实上还通过softmax函数进行转换

  a^{(i)}=q^{(i)} \times k^T{(j)}= dot* of word i and word j
  Attention(Q, K, V) = softmax(QK^T / sqrt(d_k)) V

• Step 4: A \times V = Z output matrix

  A(d_{token},d_{token}) \times V (d_{token},d_v)= Z(d_{token},d_v)

3）multiple head

输入X进入多个不同的self-attention中，得到多个（比如八个）Zmatrix后组合到一起，得到 Z(d_{token},d_m)然后进行一次linear变换得到最终输出
Z(d_{token},d_v) \times L(d_v,d_{model}) = Z(d_{token},d_{model})

4) add&norm

Add（残差连接）
– 作用：将输入直接加到输出上，公式为 ( x + F(x) )，其中 ( x )是输入，F(x) )是某一层（如Self-Attention）的输出。
– 为什么需要残差连接？ 解决深层网络中的梯度消失问题。 提供一条“捷径”，让输入信息可以直接传递到后面，避免信息丢失。

Norm（层归一化）
– 作用：对每一层的输出进行标准化处理，使得输出的均值为0，方差为1。
– 为什么需要层归一化？解决内部协变量偏移问题，稳定输入分布，加速训练并提高模型性能。

Feed Forward（前馈神经网络）
– 作用：对输入进行非线性变换，提取更复杂的特征。
– 公式：
[
\text{FFN}(x) = \text{ReLU}(xW_1 + b_1)W_2 + b_2
]
其中，( W_1, W_2 ) 是权重矩阵，( b_1, b_2 ) 是偏置项。
第一层：将输入维度扩展 d_model -> d_ff（通常 d_ff = 4 * d_model）
ReLU 或 GELU：引入非线性，使模型具有更强的特征学习能力。
第二层：将维度缩回 d_ff -> d_model，保持输入输出维度一致。

• 为什么需要Feed Forward层？ Self-Attention层主要关注序列中不同位置的关系，但对单个位置的特征提取能力有限。Feed Forward层通过非线性变换增强模型的表达能力。

2. Decoder 的结构

其解码器（Decoder）负责将编码器（Encoder）生成的表示转化为目标序列。解码器的设计使其能够高效地生成输出序列，同时考虑输入序列的上下文信息。

输入嵌入（Embedding） + 位置编码（Positional Encoding）
│
├── 掩码多头自注意力（Masked Multi-Head Self-Attention）
│ ├── 残差连接 + LayerNorm
│
├── 编码器-解码器注意力（Encoder-Decoder Attention）
│ ├── 残差连接 + LayerNorm
│
├── 前馈神经网络（FFN）
│ ├── 残差连接 + LayerNorm
│
输出层（Linear + Softmax） → 生成下一个单词

解码器的主要组成部分：

1） 掩码多头自注意力层（Masked Multi-Head Self-Attention）**

在生成序列的过程中，解码器需要确保当前位置只能关注到已生成的部分，而不能看到未来的信息。为此，掩码机制被引入，对未来的位置进行屏蔽。多头自注意力机制使模型能够从不同的子空间学习信息，提高模型的表达能力。
解码器当前生成的序列表示 X_d（维度 (d_{token}, d_{model})）,与encoder类似经过Q，K, V得到X_e

Attention(Q, K, V) = softmax((QK^T / sqrt(d_k)) + M) V
其中M是掩码矩阵

经过每个head的独立计算，得到 X_e = MultiHead(X_d) = Concat(head_1, …, head_h) W_O

2） – 编码器-解码器注意力层（Encoder-Decoder Attention）

解码器的第二个注意力层允许它关注输入序列的关键部分，以增强解码效果。它的计算方式与多头注意力类似，但 Q 来自解码器，而 K, V 来自编码器的输出 X_e。

Attention(Q, K, V) = softmax(QK^T / sqrt(d_k)) V

3）前馈神经网络

4）残差连接和层归一化

5） 词汇嵌入矩阵

logits = X \times W_{out} 得到映射到词汇表大小的向量
W_{out} (d_{model}, d_{vocab_size}), logits (d_{token},d_{vocab_size})

然后通过softmax转换为最终的概率分布，也就是每个token可能属于词汇表中的哪个单词
P = softmax(logits)

注意，在训练时，transformer一次性处理整个输入序列而不是像传统的RNN逐词生成，所以矩阵P是并行计算所有token的下一个token的预测概率，所以我们的真实标签y_{true} 也是 $(seq_len,) 形状。

举例：
输入 token 序列: [“I”, “love”, “AI”]
P[0] = 预测 “I” 的下一个 token（可能是 “love”）
P[1] = 预测 “love” 的下一个 token（可能是 “AI”）
P[2] = 预测 “AI” 的下一个 token（可能是 ““）

在 推理（inference）时，我们并不会有完整的 seq_len 输入，而是 一个一个 token 生成。这时，Transformer 采用 自回归（Autoregressive）方式，每次只关注上一个 token，并逐步扩展序列。

举例
第一步，输入 [“I”]，输出 P[0]，选取最可能的下一个词 “love”。
第二步，输入 [“I”, “love”]，输出 P[1]，选取 “AI”。
第三步，输入 [“I”, “love”, “AI”]，输出 P[2]，选取 “”

3. Transformer的结构

4. LLM的训练过程

在 LLM 训练过程中，所有上述矩阵的参数都会被 梯度下降 方法（如 AdamW 优化器）更新。训练的核心目标是 最小化语言建模损失（通常是交叉熵损失）。

训练流程：

• 输入文本：使用 E 将 token 转换为向量表示。
• 前向传播：通过 Transformer 层计算输出。
• 计算损失：使用 W_out 预测下一个 token 的概率分布，并计算交叉熵损失
  Loss = – Σ y_{true} * log(y_{pred})
• 反向传播：对所有可学习参数（W_Q, W_K, W_V, W_O, W_1, W_2, E, W_{out}）计算梯度并更新。